

Suppose we have the following temperature measurements, taken once an hour starting at 7:00 A.M. The data’s standard deviation indicates how much the data is spread around the aggregated point. You can use the methods of Sections 7.1 and 7.2 to aggregate the data by computing its mean. data have been aggregated if necessary, so only one value of y corresponds to a specific value of x. If we average the two results, the resulting data point will be x = 10V,y = 3.2 mA, which is an example of aggregating the data, In this section we assume that the.

For example, suppose we apply 10 V to a resistor, and measure 3.1 mA of current. Then, repeating the experiment, suppose We measure 3.3 mA the second time. In other cases there will be several measured values of y for a particular value of x. In some applications the data set will contain only . Suppose that x represents the independent variable in the data (such as the applied voltage in the preceding example), and y represents the dependent variable (such as the resistor current). Such plots, some perhaps using logarithmic axes, often help to discover a functional description of the data. Interpolation and extrapolation are greatly aided by plotting the data. In other cases we might need to estimate the variable’s value outside of the given data range. This process is extrapolation. In some applications we want to estimate a variable’s value between the data points. Another type of paired data represents a profile, such as a road profile (which shows the height of the road along its length). For example, the paired data might represent a cause and effect, or input-output relationship, such as the current produced in a resistor as a result of an applied voltage, or a time history, such as the temperature of an object as a function of time. The data generated by each scheme is shown in fig, along with the original input.Engineering problems often require the analysis of data pairs. The other schemes we could use are nearest, linear, and spline. Here 'cubic' is the choice for the interpolation scheme. % generate y i at x i with cubic interpolation. Step1: Generate a vector x i containing desired points for interpolation. There are two simple steps contained in interpolation: providing a list (a vector) of points at which you wish to get interpolated data and executing the appropriate function (e.g., interp1) with the desired choice for the method of interpolation. The interpolation is especially useful for periodic functions (i.e., if values of y are periodic). This is similar to interp1 except that the data is interpolated first by taking the Fourier Transform of the given data and then calculating the inverse transform using more data points. Cubic splines fit separate cubic polynomials between successive data points by matching the slopes as well as the curvature of each segment at the given data points.įast Fourier Transform (FFT)-based 1-D data interpolation. One-dimensional interpolation that uses cubic splines to find y j at desired x j,given y i at x i. To specify cubic interpolation instead of linear, for example, in interp1, use the syntax: The choice of the method dictates the smoothness of the interpolated data. The choice for the technique is nearest, linear, cubic, or spline. In each function, we have the option of specifying a method of interpolation. Vnew=interp3(x,y,z,xnew,ynew,znew,method).Īlso, there is an n-dimensional analog, interpn, if you ever need it. Given v i at (x i, y i,z i), finds v j at desired(x j,y j,z j). It is called two-dimensional interpolation because z depends on two variables, x, and y. Given z i at (x i, y i), finds z j at desired (x j,y j )from z=f(x,y).The function f is found from interpolation. Where the method is an optional argument discussed after the description of interp2 and interp3. It is called one-dimensional interpolation because y depends on a single variable x. Here f is a continuous function that is seen from interpolation. Given y i at x i, finds y j at x j from y j=f(xj ). Let us understand these functions of MATLAB one by one: interp1
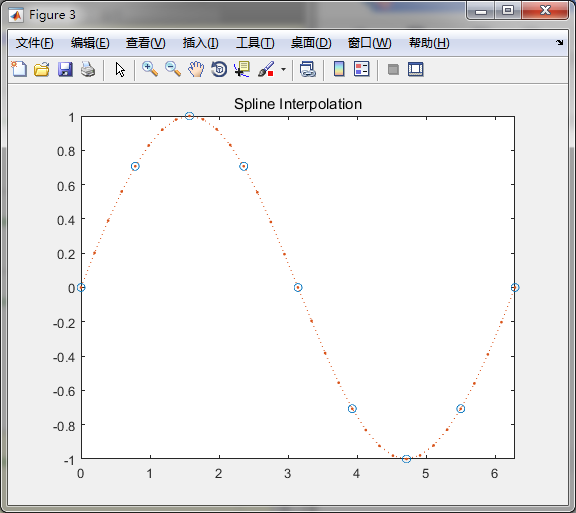
MATLAB provides the following functions to help interpolation: In MATLAB, we can interpolate our data using splines or Hermite interpolants on a fly. The most common interpolation technique is Linear Interpolation.Ī more exotic interpolation scheme is to link the data points using third degree or cubic polynomials. Interpolation is the process of describing a function which "connects the dots" between specified (data) points.


 0 kommentar(er)
0 kommentar(er)
